Introduction

Lithuania’s electoral system is complex with the Parliament formed in part by a multi-member constituency elected by proportional representation and by a nearly-equal-sized collection of single-member constituencies which are elected with two-round ballots.

It is proverbially difficult to predict, given little polling, large errors, a low threshold for entry into the multi-member constituency, a large number of active parties, rapid evolution (creation and dissolution) of parties and a short historical trend.

Lithuania’s most recent parliamentary elections were held in October 2020 — the first round on 11 October and the second round on 25 October.

In October 2020 I tried to predict the outcome of the second round of voting in the single-member constituencies based on historical data from elections in 2012 and 2016 and on the results of the first round of voting in the single-member constituencies.

I made a presentation of those predictions and published it shortly after polls closed in round II. Here I compare those predictions (and the assumptions) with the actual results.

Summary

My system worked quite well.

I predicted the overall winner, and was within 10% of their seat count; for the TS-LKD I predicted 54 seats and they won 50.

I underestimated that LRLS by two seats (they won 13) and underestimated the success of independent candidates, predicting that 2 would win their seats when 4 did.

For the LSDDP I predicted 2 seats and they won 3; for the LVŽS I predicted 33 seats and they won 32.

For the LT, LRRA, LP, DP, LŽP and LSDP I correctly predicted their seat counts (39 seats correctly allocated across 6 parties).

Out of 141 seats, the absolute error was 10 seats — but 73 of the seats had been won in the first round, so my prediction was only considering the remaining 68 seats.

Party Actual Prediction Difference
TS-LKD 50 54 -4
LT 1 1 0
LLRA 3 3 0
Ind. 4 2 +2
LRLS 13 11 +2
LP 11 11 0
DP 10 10 0
LŽP 1 1 0
LSDP 13 13 0
LSDDP 3 2 +1
LVŽS 32 33 -1

Approach

My system uses a two pass approach to predict winners in each of the seats being contested in the second round.

Part A assumes that seats which meet certain criteria will be won by the candidate who won in the first round.

Part B uses a Monte Carlo approach to calculate the probability that each leading candidate in the remaining seat will win the second round, then simulates these elections in each constituency many times to approximate the distribution of all the seats.

Before the election I used this to determine the expected number of seats won by each party (given in the prediction column above) and generate histograms showing the expected frequency of each outcome by party.

Reviewing the data after the election I realised that my simulation showed that a coalition of the TS-LKD, LRLS and LP had a 99.96% chance of winning more than 71 seats. This coalition won 74 seats and is forming a government after the election.

Background

Lithuania uses a mix of a proportional representation and single-member constituencies with a run-off.

Advance polling might allow prediction of the make-up of the multi-member constituency, but polling errors are large compared to the threshold for winning any seats in the multi-member constituency and in 2020 there were surprises in the first round.

Results of the first round may give a heuristic indicator of the eventual outcomes in the run-offs, based on results in 2012 and 2016.

Round I

After the first round of polling, seats are assigned in the multi-member constituency based on proportional representation with a 5% threshold which parties must reach to win any seats. If they pass this threshold, they will get at least 6 seats.

These form the “floor” of a party’s eventual representation in Parliament. They cannot have fewer than the seats they get in the multi-member constituency.

A separate ballot in the first round of polling lets Lithuanians choose among candidates for their local constituency MP.

If a candidate in a constituency wins more than 50% of the vote, they are elected to their seat.

If no candidate gets 50% or more, the top two candidates compete in a run-off Round II, two weeks later.

Round II

Considering Round II, parties now have a “ceiling” on how many seats they can win.

This isn’t just the number of seats they placed first in Round I, but also includes those where they were the first runner-up.

In this discussion the leader is the candidate who won the most votes in the first round. The challenger is the first runner-up — the candidate who won the second-most number of votes in the first round and who contests the second round run-off with the leader.

The winner in each constituency has the most votes in the second round run-off, or won more than 50% of the votes in the first round and does not face a run-off.

Most candidates who win in Round I win in Round II, but not all.

First Round Winners

In the single-member constituencies, any candidate who wins more than 50% of the vote in the first round is immediately elected. They are the winner.

If no candidate wins 50%, the top two ranked candidates go to a run-off election two weeks later (as leader and challenger).

In 2020, three candidates won single member constituency seats in the first round.

Candidate Constituency Party Vote Share
INGRIDA ŠIMONYTĖ Antakalnio Tėvynės sąjunga – Lietuvos krikščionys demokratai 62.6
BEATA PETKEVIČ Šalčininkų–Vilniaus Lietuvos lenkų rinkimų akcija - Krikščioniškų šeimų sąjunga 62.2
ČESLAV OLŠEVSKI Medininkų Lietuvos lenkų rinkimų akcija - Krikščioniškų šeimų sąjunga 55.8

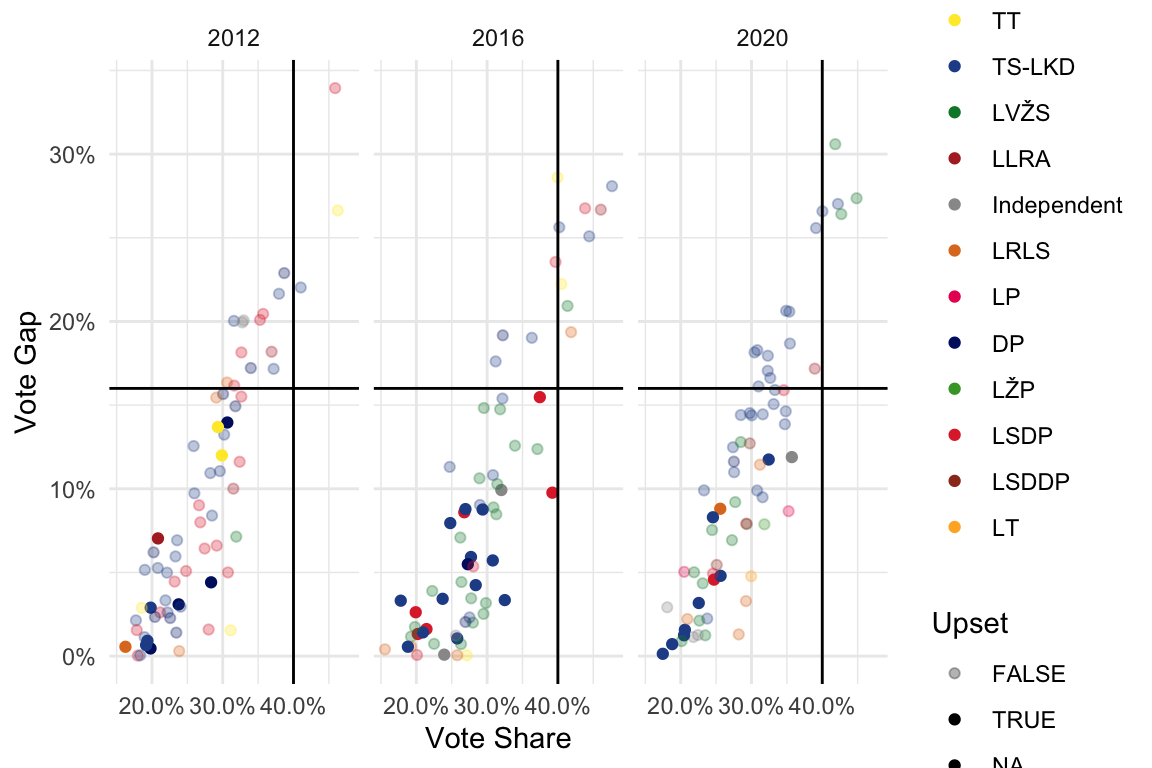
Vote shifts from Round I to Round II

Graphical comparison of the votes won by the top two candidates in Round I and Round II in the 2012 and 2016 elections showed distinct party-by-party behavior depending on the party of the first round winner.

In particular, TS-LKD candidates fared very badly in the second round in 2016.

Compared with previous years, there was much less difference in how leading candidates fared based on their party affiliation.

Vote shifts in 2020

Vote shifts in 2016

Vote shifts in 2012

Rose Graphs

These graphs try to present an overview of how votes are split among several parties in the first and s`econd rounds. The radial distance indicates the vote share won by each candidate in the first round. The circles indicate the vote share won by the leader and challenger in the second round. Parties are arranged in an arbitrary but consistent order intended to emphasise policy separtion between parties.

Part A | Vote share and Vote lead

Based on results from the 2012 and 2016 elections, two thresholds were established to determine that leaders would be assumed to win the second-round:

In 2012 and 2016, all leaders who gained more than 40% of the vote in the first round won in the second round.

Many leaders with less than 40% of the vote won in both rounds.

Looking at graphs of two indicators, it was apparent that leaders whose lead over the challenger was more than 16% also all won in the second round.

In 2020, these criteria account for around 20 seats in the single member constituencies.

These empirical assumptions can be given some explanation. A 16% lead over a challenger, where the leader has less than 40% of the vote, means that the challenger has at most 24% of the vote and — in a multiparty system such as Lithuania’s — likely has less. The leader already has 5/3 times as many votes as the challenger.

First round vote share

Predictions | Part A

We looked at the 68 seats being contested in Round II in 2020.

For those where the first round winner has 40% of the vote or who lead their opponents by 16% we will assume they will win the second round.

This gives 16 outcomes.

Party Seats
LLRA 1
LVŽS 3
TS-LKD 12

Every one of these candidates did win in the second round.

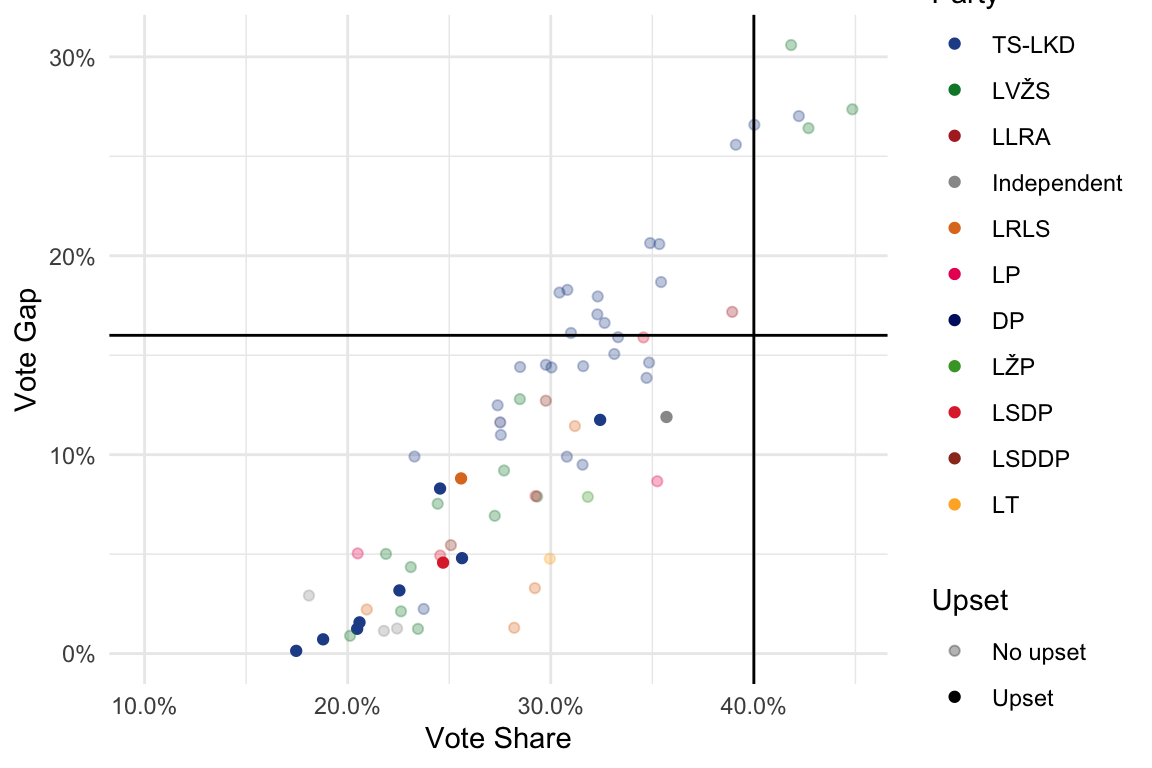
Part A | List

Constituency First Round Vote Share (%) Party
2. Naujamiesčio–Naujininkų 32.31129 TS-LKD
4. Žirmūnų 39.11286 TS-LKD
7. Justiniškių–Viršuliškių 30.81669 TS-LKD
8. Pilaitės–Karoliniškių 30.99478 TS-LKD
9. Lazdynų 34.89190 TS-LKD
10. Naujosios Vilnios 35.34312 TS-LKD
11. Panerių–Grigiškių 30.42785 TS-LKD
12. Verkių 42.21479 TS-LKD
17. Petrašiūnų–Gričiupio 35.43172 TS-LKD
20. Centro–Žaliakalnio 40.02344 TS-LKD
39. Žemaitijos šiaurinė 44.84981 LVŽS
44. Radviliškio–Tytuvėnų 32.29268 TS-LKD
45. Šiaulių krašto 42.69021 LVŽS
47. Žiemgalos rytinė 32.65018 TS-LKD
52. Nalšios šiaurinė 41.83574 LVŽS
55. Nemenčinės 38.93504 LLRA

Predictions | Part B

What about the other 52 seats?

85% of leaders won the second round in 2012 and 69% of leaders won the second round in 2016, but this masks wide variation among parties and between years.

TS-LKD retained their lead in 87.5% times in 2012 but only 40% in 2016

Success rates for parties in 2020 are much more like those in 2012. Two larger parties (LSDP and TS-LKD) went on to win less than 46% of the seats where they were leaders going into the run-off.

In 2020, TS-LKD were leaders going into half of the run-offs and own 77% of them. LSDP won 3 of the 4 competitions they were leading in.

This suggests that the estimates of probability of winning in run-offs used in the Monte Carlo simulations were low. They were based on results from 2012 and 2016 — and 2020 looks more like 2012.

Part B | Vote shifts?

I’ll try applying a Monte Carlo approach using estimates of probability of winning a run-off and then simulating this multiple times.

First, we’ll average the probability of a party winning a run-off across the 2012 and 2016 elections.

Party Won Lost Total Success Rate (%)
DP 11 5 16 68.75000
Independent 6 3 9 66.66667
LLRA 4 1 5 80.00000
LP 2 0 2 100.00000
LRLS 11 2 13 84.61538
LS 1 0 1 100.00000
LSDDP 2 0 2 100.00000
LSDP 25 7 32 78.12500
LT 1 0 1 100.00000
LVŽS 34 0 34 100.00000
LŽP 1 0 1 100.00000
TS-LKD 57 23 80 71.25000
TT 6 1 7 85.71429

Adjusted success rates

The earlier success rates for the 2012 and 2016 elections gave an overestimate, because they included the sure wins already accounted for in part A, so adjusted success rates for each leader party were calculated excluding those conditions accounted for in part A.

These only accounted for parties which had competed as leaders or challengers in 2012 and 2016, leaving out the LP, LT, LSDDP and LŽP. (All but the LŽP were newly-formed parties.)

Party Won Lost Total Success Rate (%)
DP 7 5 12 58.33333
Independent 1 2 3 33.33333
LLRA 1 1 2 50.00000
LRLS 5 1 6 83.33333
LS 1 0 1 100.00000
LSDP 15 6 21 71.42857
LVŽS 20 0 20 100.00000
TS-LKD 22 15 37 59.45946
TT 3 1 4 75.00000

We’ll apply a maximum of 80% and assign a typical chance of success of 60% where we don’t have earlier data.

Party Won Lost Total Success Rate (%) Probability
DP 7 5 12 58.33333 58.33333
Independent 1 2 3 33.33333 33.33333
LLRA 1 1 2 50.00000 50.00000
LRLS 5 1 6 83.33333 80.00000
LS 1 0 1 100.00000 80.00000
LSDP 15 6 21 71.42857 71.42857
LVŽS 20 0 20 100.00000 80.00000
TS-LKD 22 15 37 59.45946 59.45946
TT 3 1 4 75.00000 75.00000
LP 0 0 0 NA 60.00000
LT 0 0 0 NA 60.00000
LSDDP 0 0 0 NA 60.00000
LŽP 0 0 0 NA 60.00000

Simulate \(5\times 10^{4}\) times

The second round of the election was simulated 510^{4} times. Essentially a weighted coin was flipped for each constituency in each simulated election.

The probability of the leader winning is given by the adjusted probabilities we have calculated — if they lose, the challenger wins the seat.

The many simulations were then compiled to see how many seats on average the party will win — the “expected” number of seats

Expected numbers of seats

These were the calculated numbers of seats from the Monte Carlo simulations.

Party ExpectedSeats Rounded
DP 0.58396 1
Independent 2.01430 2
LP 3.23392 3
LRLS 5.07038 5
LSDDP 1.87766 2
LSDP 5.39150 5
LT 0.60188 1
LVŽS 13.79122 14
LŽP 0.59760 1
TS-LKD 18.42154 18
All 51.58396 52

Note that these only correspond to the 68 seats assigned in Part B.

These figures could also be calculated arithmetically.

\(\begin{aligned} \langle n_\mathrm{TS-LKD} \rangle & = \sum_\text{Seats where TS-LKD is leader}P(\text{TS-LKD}) + \sum_\text{Seats where TS-LKD is challenger}(1-P(\text{leader})) \\ & = 35 \cdot P(\text{TS-LKD}) + 2 \cdot (1-P(\text{Independent})) \\ & + (1-P(\text{LSDDP})) + (1-P(\text{LP})) + (1-P(\text{LT})) \\ & + 3 \cdot (1-P(\text{LRLS})) + (1-P(\text{LLRA})) \\ & + 10 \cdot (1-P(\text{LVŽS})) \end{aligned}\)

A more straightforward case is for the LRLS (which was competing in fewer seats):

\(\begin{aligned} \langle n_\mathrm{LRLS} \rangle & = \sum_\text{Seats where LRLS is leader}P(\text{LRLS}) + \sum_\text{Seats where LRLS is challenger}(1-P(\text{leader})) \\ & = 5 \cdot P(\text{LRLS}) + (1-P(\text{LSDP})) + 3 \cdot (1-P(\text{TS-LKD})) \\ & = 5 (0.80) + (1-0.71) +3 (1-0.59) \\ &= 5.52 \end{aligned}\)

Histograms of Seat Allocation

Histograms show the distribution of the different numbers of seats for each party.

The lump being further right means that the party is likely to win more seats. A narrow lump indicates that the party’s chances are limited in a tight range.

The histograms for the LT, DP and LŽP parties are not very useful. They roughly show that the party has about a 60% chance of winning the seat where they are leading, but this is determined for the LT and LŽP parties by the guess we made about how “new” parties would do.

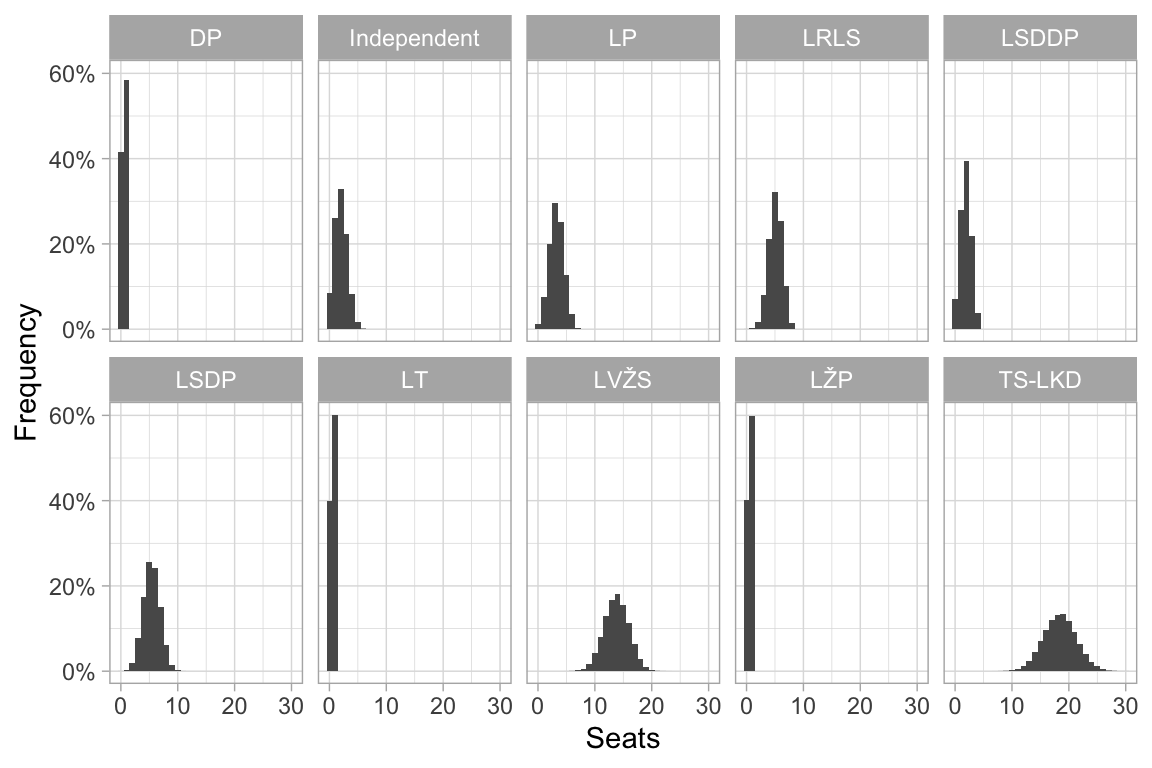
After \(5\times 10^{4}\) simulations.

Other calculated probabilities

Possible coalitions

What I did not think to do before the second round-results were announced was look at what might be the chances of various possible coalitions.

Had I done so, I might have realised that the three (roughly) Centre-Right parties of the TS-LKD, LRLS and LP together had a better than 99% chance of winning 71 or more seats. Together they won 74 seats and are forming a coalition government.

Below is a histogram indicating probability of seat distributions for Centre-Right (TS-LKD, LRLS, LP) and Centre-Left (LSDP, LSDDP, LŽP) coalitions, and for the existing coalition (LVŽS, LLRA, LSDDP).

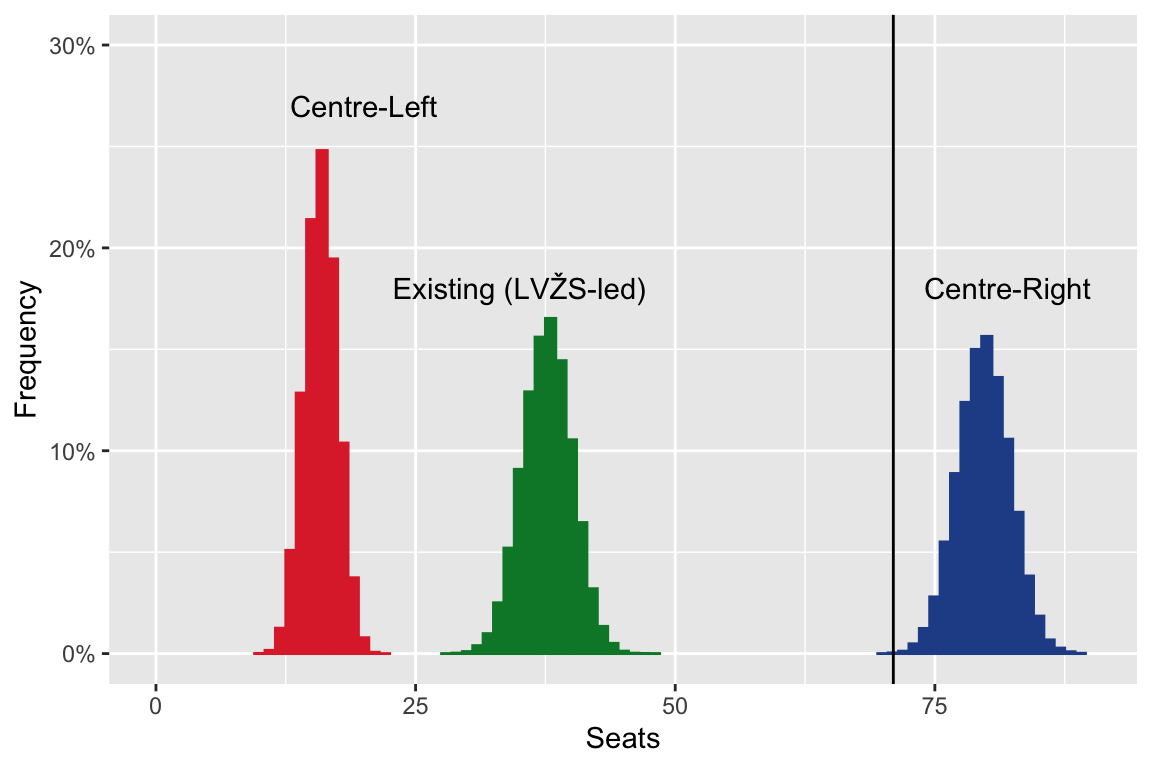
Results

Predictions

Results

Note that party ordering has been shifted in the results to reflect new alignments after the elections.

Next steps

It may be interesting to see whether assigning the same probability of success to all leaders regardless of their party affiliation may give better results.

I would still like to try working to predict outcomes of the first round of voting in both the multi-member constituency (hampered by polls with many “undecided” voters and wide margins of error) and single-member constituencies (hampered by a lack of regional polls). This could be done looking at historical voting behaviour in each constituency (or even each polling precinct) and comparing it with national polls and results in the multimember constituency. Lithuanians can and do split their ballot between a selection of a party list at the national level (in the multimember constituency) and preference for an individual candidate at the single-member constituency level and this would be interesting to explore in more detail.

Party key

Party Name Seats
TS-LKD Tėvynės sąjunga - Lietuvos krikščionys demokratai 51
LVŽS Lietuvos valstiečių ir žaliųjų sąjunga 32
DP Darbo partija 10
LSDP Lietuvos socialdemokratų partija 13
LP Laisvės partija 11
LRLS Lietuvos Respublikos liberalų sąjūdis 13
LLRA Lietuvos lenkų rinkimų akcija - Krikščioniškų šeimų sąjunga 3
Independent Independent 4
LSDDP Lietuvos socialdemokratų darbo partija 3
LT Partija „Laisvė ir teisingumas“ 1
LŽP Lietuvos žaliųjų partija 1

References and credits

Data is from the Central Election Commission of the Republic of Lithuania, particularly their Elections home page (Rinkėjo puslapis) which presents historical electoral data in a consistent and open way.

Hemicycle charts were created using Filip Van Laenen’s Scalable Hemicycle Charts (SHecC)

All analysis was done with R, mostly using the tidyverse collection of packages.